Introduction au Dataset MNIST
Le dataset MNIST est une référence incontournable dans le domaine du machine learning et de la vision par ordinateur. Il contient des images manuscrites des chiffres de 0 à 9, chacune en niveaux de gris et de (très) petite taille (28×28 pixels).
Les données sont réparties en 60 000 images d’entraînement et 10 000 images de test, et sont principalement utilisées pour les tâches de classification.
Ce dataset a été conçu pour simplifier les expérimentations sur les modèles de deep learning, mais une petite difficulté technique réside dans le fait que les données sont encodées et compressées dans un format spécifique (IDX). Ce format nécessite une étape de décompression et de lecture avant de pouvoir être utilisé.
Heureusement, avec Python, il est possible de charger et de manipuler le dataset MNIST facilement. Ces fichiers sont au format IDX. Pour les utiliser en Python, vous pouvez les charger et les prétraiter à l’aide de la bibliothèque TensorFlow.
TensorFlow offre une méthode pratique pour importer directement le jeu de données MNIST sans avoir à le télécharger manuellement.
from tensorflow.keras.datasets import mnist # Télécharger et sauvegarder le dataset MNIST (x_train, y_train), (x_test, y_test) = mnist.load_data()
Le dataset MNIST est téléchargé dans un répertoire temporaire par défaut utilisé par TensorFlow. Ces fichiers ne sont pas automatiquement placés votre répertoire de travail de votre script. Vous pouvez si vous le souhaitez sauvegarder les data dans votre répertoire.
# Définir les chemins pour sauvegarder les fichiers du dataset
dataset_save_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/mnist_data.npz'
# Télécharger et sauvegarder le dataset MNIST
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Sauvegarder les données dans un fichier compressé
np.savez_compressed(dataset_save_path, x_train=x_train, y_train=y_train, x_test=x_test, y_test=y_test)
print(f"Dataset MNIST sauvegardé sous : {dataset_save_path}")
Chaque image est de taille 28×28 pixels. Les valeurs de pixels sont des nuances de gris et vont de 0 (noir) à 255 (blanc).
Les labels associés indiquent le chiffre manuscrit représenté sur chaque image.
Ci-dessous l’image a été agrandie : 512*512 pixels.
Les applications historiques de MNIST incluent son usage dans le domaine bancaire, notamment pour l’automatisation de la reconnaissance des chiffres manuscrits sur les chèques.
Le choix (simple) d’un DNN (Deep Neural Network)
Un DNN est un réseau de neurones dense composé uniquement de couches pleinement connectées (Dense layers). Les données sont représentées sous forme de vecteurs plats (1D). Dans le cas de MNIST : Les images de taille (28, 28) sont converties en vecteurs de taille 784 (28 * 28).
Cela se fait par un processus appelé flattening (aplatissement). Aucun canal comme la profondeur de couleur n’est utilisé (comme c’est le cas avec un CNN).
Comment choisir le (bon) nombre de paramètres ?
Un paramètre dans un réseau de neurones est une valeur qui est mise à jour au cours de l’entraînement pour améliorer les prédictions du modèle. Ces paramètres incluent :
- Poids (weights) : Les connexions entre les neurones. Chaque neurone d’une couche est connecté à chaque neurone de la couche suivante, et ces connexions sont associées à des poids.
- Biais (bias) : Une valeur ajoutée à la somme pondérée des entrées avant de passer l’activation.
La répartition des neurones suit une structure en « entonnoir », avec un nombre décroissant de neurones dans les couches successives. On peut commencer avec un petit réseau et vérifier si les performances (accuracy, loss) augmentent de manière empirique par « tâtonnement ».
Pour le dataset MNIST, on peut commencer avec une seule couche dense de 128 neurones.
Calcul pour chaque couche dense (exemple) :
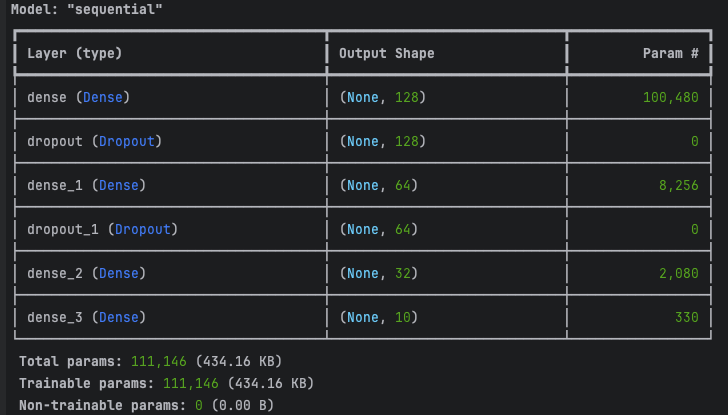
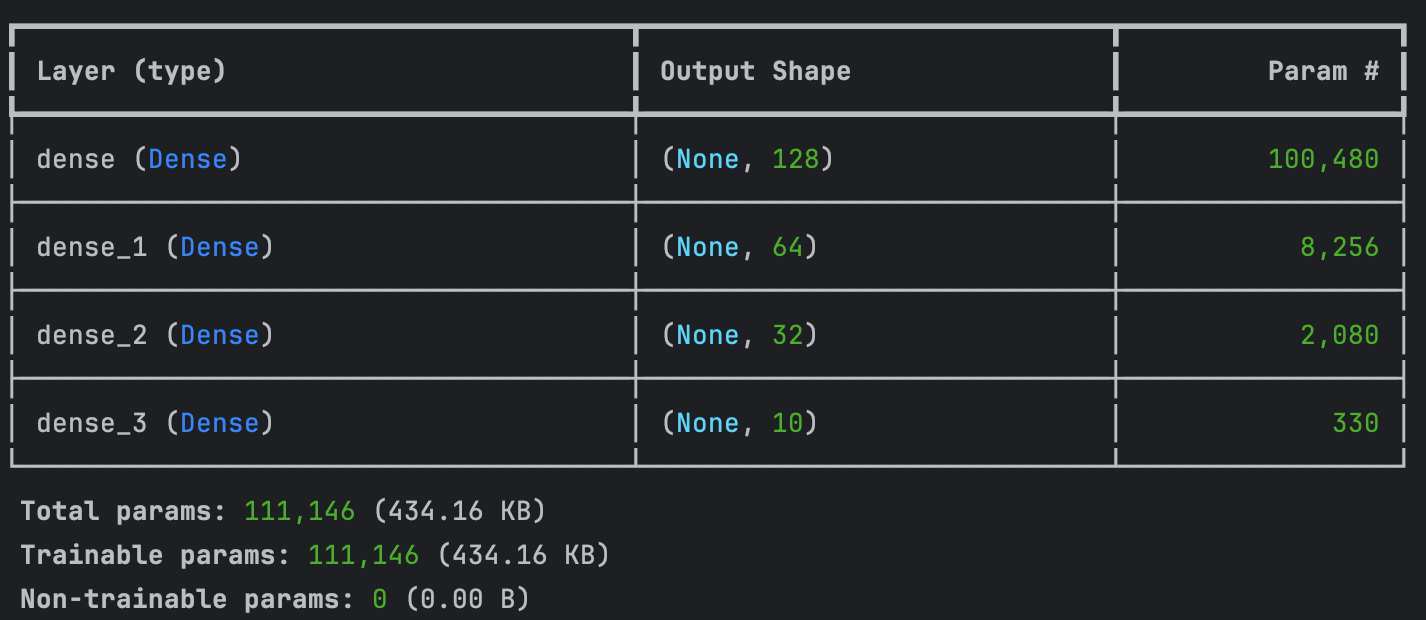
Analysons la répartition des paramètres pour ce modèle DNN avec les couches spécifiées :
Couche (Dense, 128 neurones)
Entrée : 28×28 = 784 (dimensions des images aplaties en vecteurs).
Paramètres = (784×128) + 128 = 100 480 paramètres
Couche 1 (Dense, 64 neurones)
Entrée : 128 (sortie de la couche précédente).
Paramètres : Chaque neurone de cette couche est connecté aux 128 neurones précédents.
Paramètres = (128×64) + 64 = 8 256 paramètres
Couche 2 (Dense, 32 neurones)
Entrée : 64 (sortie de la couche précédente).
Paramètres : Chaque neurone est connecté aux 64 neurones précédents.
Paramètres = ( 64×32) + 32 = 2 112 paramètres
Couche 3 (Dense, 10 neurones)
Entrée : 32 (sortie de la couche précédente).
Paramètres : Chaque neurone est connecté aux 32 neurones précédents.
Paramètres = (32×10) + 10 = 330 paramètres
Il est important de conserver la couche de sortie (« couche dense_3 » avec 10 neurones car nous avons 10 labels (10 chiffres à prédire).
Sortie : 10 neurones pour les 10 classes/labels (0-1-2-3-4-5-6-7-8-9).
Vous pouvez modifier la logique / paramétrage de ces 4 couches et observer si il y a une différence significative en terme de précision du modèle sur les données de test.
Avec le paramétrage de ces couches ci-dessous vous obtiendrez une précision de 97%.
# Construction du modèle DNN
model = models.Sequential([
layers.Dense(128, activation='relu', input_shape=(28 * 28,)),
# layers.Dropout(0.2),
layers.Dense(64, activation='relu'),
# layers.Dropout(0.2),
layers.Dense(32, activation='relu'),
layers.Dense(10, activation='softmax')
])
Vous remarquez ci-dessous que la couche « layers.Dropout » a été désactivée simplifiant la construction du modèle.
# Construction du modèle DNN
model = models.Sequential([
layers.Dense(128, activation='relu', input_shape=(28 * 28,)),
# layers.Dropout(0.2),
layers.Dense(64, activation='relu'),
# layers.Dropout(0.2),
layers.Dense(32, activation='relu'),
layers.Dense(10, activation='softmax')
])
L’hyperparamètre Dropout est une technique de régularisation qui désactive aléatoirement un pourcentage des neurones lors de l’entraînement pour réduire la dépendance du modèle à certaines connexions. Cette régularisation est particulièrement utile pour les datasets complexes ou de grande taille où le risque de sur-apprentissage est élevé.
Avec layers.Dropout(0.2), 20% des neurones d’une couche sont désactivés de manière aléatoire à chaque étape d’entraînement. Par exemple pour une couche dense de 128 neurones, 20% de ces neurones sont désactivés, ce qui correspond à : 128×0.2 = 25.6 (soit 26). Ces neurones désactivés ne contribuent pas à la sortie de la couche pendant cette étape d’entraînement (batch_size).
# Entraînement du modèle
history = model.fit(
x_train, y_train,
epochs=10,
batch_size=32,
validation_data=(x_test, y_test)
)
Cette désactivation est aléatoire signifiant que les neurones désactivés changent à chaque étape d’entraînement.
Le but de Dropout est d’empêcher les neurones de devenir trop spécialisés (dépendance excessive entre eux) ou de mémoriser les données d’entraînement.
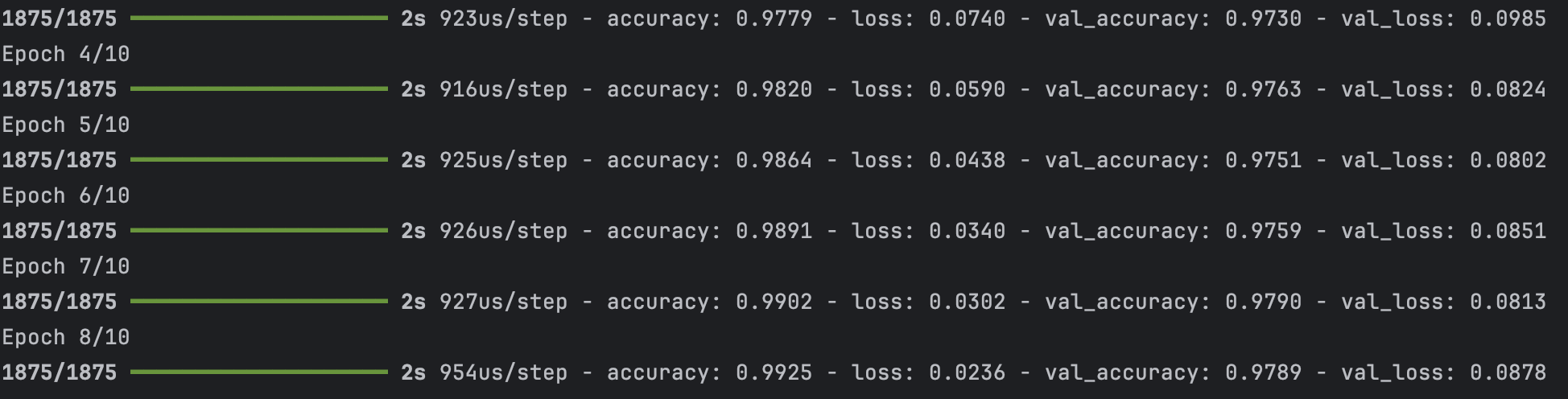
Une étape d’entraînement (ou batch) est différente d’un epoch. Une étape correspond à l’entraînement du modèle sur un lot (batch) de données (ici un lot d’images). Par exemple, avec le dataset MINST de 60 000 images et qu’on paramètre une taille de batch de 32, chaque étape d’entraînement traite 32 exemples à la fois.
L’hyperparamètres « Epoch » correspond à une passe complète de tout le dataset. Si une epoch contient les paramètres de 60 000 images (la taille totale du dataset d’entraînement MNIST). Pour connaitre le nombre d’étape on divise les images en batch (lots) de taille 32 (32 images), un epoch contient 1875 étapes, et chaque étape traite un batch de 32 images.
Les couches d’activation
On voit que dans chaque couche de neurones on une fonction d’activation (fonction d’activation qui est un paramètres très important dans le deeplearning).
# Construction du modèle DNN
model = models.Sequential([
layers.Dense(128, activation='relu', input_shape=(28 * 28,)),
# layers.Dropout(0.2),
layers.Dense(64, activation='relu'),
# layers.Dropout(0.2),
layers.Dense(32, activation='relu'),
layers.Dense(10, activation='softmax')
])
La dernière couche du modèle a 10 neurones, correspondant aux 10 classes possibles de MNIST (les chiffres de 0 à 9). L’activation « softmax » est utilisée ici pour transformer les sorties de cette couche en une distribution de probabilités.
Chaque sortie représente la probabilité que l’image appartient à une classe particulière.
Par exemple, si l’entrée est une image du chiffre « 3 », Softmax pourrait produire une sortie comme :
[0.01, 0.02, 0.01, 0.90, 0.01, 0.02, 0.01, 0.01, 0.00, 0.01]
Par exemple, ici, la probabilité maximale est associée à la classe « 3 » (90%).
Le code source
Le script génère aléatoirement des représentations d’images utilisées lors de l’entraînement, accompagnées de leurs labels correspondants. Ces exemples sont sauvegardés au format PNG dans le répertoire de travail.
Ensuite, une série d’images, sélectionnées (toujours aléatoirement) à partir de l’ensemble de test, est affichée avec les prédictions de leurs labels correspondants.
Enfin, le modèle ayant une précision de 97 % (ce score pourrait être amélioré avec un CNN), le script extrait une série d’images pour lesquelles le modèle s’est trompé dans ses prédictions.
Certaines erreurs peuvent sembler « aberrantes », mais elles reflètent les limites actuelles du modèle.
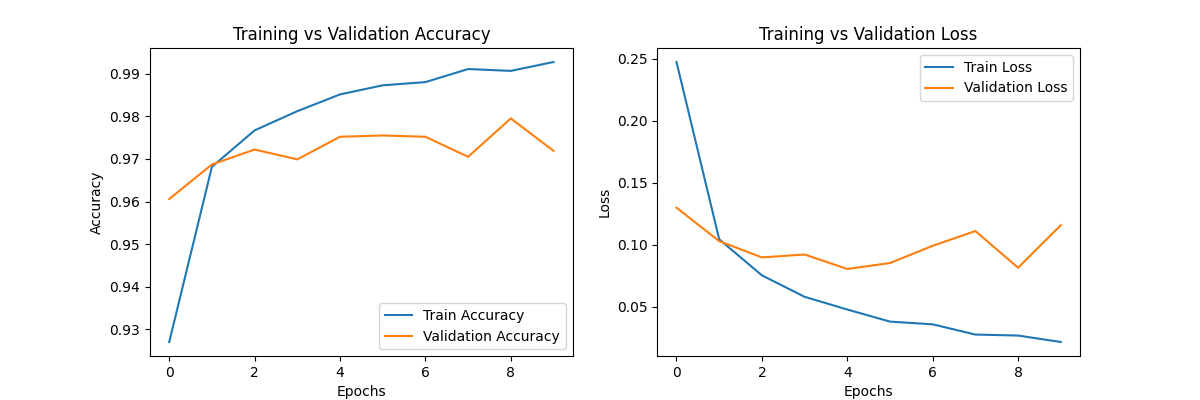
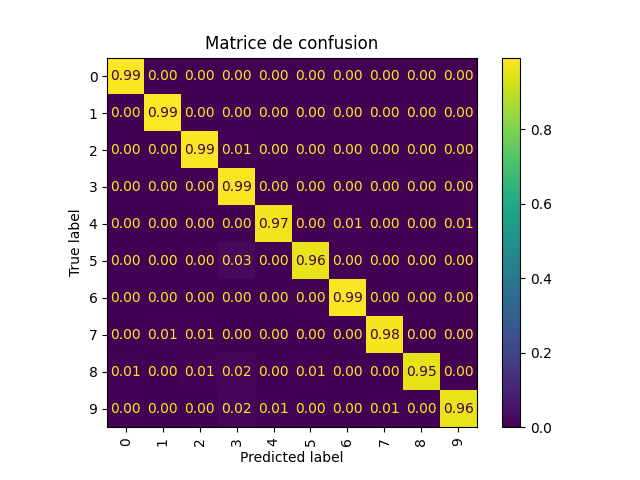
En complément des courbes « accuracy » et « loss » présentées plus haut dans l’article, la matrice de confusion vous offre une vue détaillée des chiffres pour lesquels le modèle manque de précision dans ses prédictions.
Le script python
Le script s’exécute en local, il vous suffit de redéfinir le chemin vers votre répertoire de travail.
# pip install tensorflow matplotlib numpy scipy pandas scikit-learn
import os
import random
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from tensorflow.keras import layers, models
from tensorflow.keras.datasets import mnist
# Définir les chemins pour sauvegarder les fichiers
model_save_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/mnist_DNN_model.h5'
metrics_save_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/training_metrics.txt'
accuracy_plot_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/accuracy_plot.png'
loss_plot_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/loss_plot.png'
train_images_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/train_sample_images.png'
test_images_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/test_sample_images.png'
errors_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/error_samples.png'
confusion_matrix_path = '/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/confusion_matrix.png'
os.makedirs(os.path.dirname(model_save_path), exist_ok=True)
# Télécharger et charger le dataset MNIST
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Affichage de la répartition des données
print("x_train : ", x_train.shape)
print("y_train : ", y_train.shape)
print("x_test : ", x_test.shape)
print("y_test : ", y_test.shape)
# Sauvegarde de 5 images aléatoires en fichiers individuels
random_indices = random.sample(range(x_train.shape[0]), 5)
for i, idx in enumerate(random_indices):
image_path = f"/Users/stephanemeurisse/Documents/Recherche/DNN-dataset-MNIST/sample_image_{i + 1}.png"
img = Image.fromarray(255 - x_train[idx]) # Inverser les couleurs pour fond blanc
img.save(image_path)
print(f"Image sauvegardée sous : {image_path}")
# Affichage de 10 images aléatoires d'entraînement avec leurs labels
train_images_2_show = []
train_titles_2_show = []
for i in range(10):
r = random.randint(0, x_train.shape[0] - 1)
train_images_2_show.append(255 - x_train[r]) # Inverser les couleurs pour fond blanc
train_titles_2_show.append(f"Training image [{r}] = {y_train[r]}")
plt.figure(figsize=(15, 8))
for i, (image, title) in enumerate(zip(train_images_2_show, train_titles_2_show)):
plt.subplot(2, 5, i + 1)
plt.imshow(image, cmap='gray')
plt.title(title)
plt.axis('off')
plt.tight_layout()
plt.savefig(train_images_path)
print(f"Images d'entraînement sauvegardées sous : {train_images_path}")
# Affichage de 10 images aléatoires de test avec leurs labels
test_images_2_show = []
test_titles_2_show = []
for i in range(10):
r = random.randint(0, x_test.shape[0] - 1)
test_images_2_show.append(255 - x_test[r]) # Inverser les couleurs pour fond blanc
test_titles_2_show.append(f"Test image [{r}] = {y_test[r]}")
plt.figure(figsize=(15, 8))
for i, (image, title) in enumerate(zip(test_images_2_show, test_titles_2_show)):
plt.subplot(2, 5, i + 1)
plt.imshow(image, cmap='gray')
plt.title(title)
plt.axis('off')
plt.tight_layout()
plt.savefig(test_images_path)
print(f"Images de test sauvegardées sous : {test_images_path}")
# Normalisation et mise en forme des données
x_train = x_train.reshape(-1, 28 * 28) / 255.0
x_test = x_test.reshape(-1, 28 * 28) / 255.0
# Conversion des labels en one-hot encoding
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)
# Construction du modèle DNN
model = models.Sequential([
layers.Dense(128, activation='relu', input_shape=(28 * 28,)),
# layers.Dropout(0.2),
layers.Dense(64, activation='relu'),
# layers.Dropout(0.2),
layers.Dense(32, activation='relu'),
layers.Dense(10, activation='softmax')
])
model.summary()
# Compilation du modèle
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Entraînement du modèle
history = model.fit(
x_train, y_train,
epochs=10,
batch_size=32,
validation_data=(x_test, y_test)
)
# Évaluation du modèle
loss, accuracy, = model.evaluate(x_test, y_test)
print(f"Test Loss: {loss:.4f}")
print(f"Test Accuracy: {accuracy:.4f}")
# Sauvegarde des métriques dans un fichier texte
with open(metrics_save_path, 'w') as f:
f.write(f"Test Loss: {loss:.4f}\n")
f.write(f"Test Accuracy: {accuracy:.4f}\n")
# Visualisation et sauvegarde des courbes de performance
plt.figure(figsize=(12, 4))
# Courbe d'Accuracy
plt.subplot(1, 2, 1)
plt.plot(history.history['accuracy'], label='Train Accuracy')
plt.plot(history.history['val_accuracy'], label='Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.title('Training vs Validation Accuracy')
plt.savefig(accuracy_plot_path)
# Courbe de Loss
plt.subplot(1, 2, 2)
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.title('Training vs Validation Loss')
plt.savefig(loss_plot_path)
print(f"Courbes sauvegardées sous '{accuracy_plot_path}' et '{loss_plot_path}'")
# Sauvegarde du modèle
model.save(model_save_path)
print(f"Modèle sauvegardé sous '{model_save_path}'")
# Prédictions sur un jeu de test
predictions = model.predict(x_test)
y_pred = np.argmax(predictions, axis=1)
y_true = np.argmax(y_test, axis=1)
# Identification des erreurs
errors = [i for i in range(len(x_test)) if y_pred[i] != y_true[i]]
errors = errors[:min(24, len(errors))]
# Affichage des erreurs avec les prédictions en couleur
plt.figure(figsize=(12, 8))
for i, idx in enumerate(errors[:15]):
plt.subplot(3, 5, i + 1)
plt.imshow(255 - x_test[idx].reshape(28, 28), cmap='gray') # Inverser les couleurs pour fond blanc
plt.title(f"True: {y_true[idx]} Predict: {y_pred[idx]}", color='red')
plt.axis('off')
plt.tight_layout()
plt.savefig(errors_path)
print(f"Images d'erreurs sauvegardées sous : {errors_path}")
# Matrice de confusion
cm = confusion_matrix(y_true, y_pred, normalize='true')
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=range(10))
disp.plot(cmap='viridis', xticks_rotation='vertical', values_format=".2f")
plt.title('Matrice de confusion')
plt.savefig(confusion_matrix_path)
plt.show()
print(f"Matrice de confusion sauvegardée sous : {confusion_matrix_path}")
print("Exécution terminée.")
Voilà, c’est terminé !
Encore un article (trop) long, qui aurait pu être encore plus long si j’avais passé en revue tous les hyperparamètres du modèle.
À noter qu’à l’issue de l’entraînement, le modèle est sauvegardé dans votre répertoire de travail.