Toute bonne chose a une fin… Il était temps de mettre un point final à cet article. Il s’agit ici d’une démarche exploratoire visant à croiser, pour l’analyse textuelle, plusieurs méthodes d’embedding de BERT, une analyse de similarité cosinus et une analyse de centralité (théorie des graphes). Ça fait déjà beaucoup de choses !
Dans l’analyse textuelle, il est possible de construire un graphe lexical à partir des cooccurrences de mots sans recourir aux techniques d’embedding. Cependant, dans cet article, nous allons expérimenter le processus d’embedding en utilisant CamemBERT. Cette approche permet de transformer les mots en vecteurs numériques qui capturent leur similarité sémantique, et de construire ensuite un graphe où les liens, définis via le cosinus de similarité, offrent une vision des relations implicites dans le corpus.

Par ailleurs, nous explorerons comment diverses formules mathématiques – telles que la moyenne simple (mean pooling), la méthode max pooling et le SIF pooling – permettent de « pondérer » les termes lors de leur vectorisation, en mettant notamment en exergue l’importance des mots moins fréquents de manière similaire à une pondération TF‑IDF.
Il n’existe pas de mode d’embedding universellement supérieur, mais le choix de la méthode doit être guidé par les besoins spécifiques de votre analyse.
Ainsi, bien que la théorie des graphes puisse s’appliquer à des mesures issues des cooccurrences ou d’autres tests statistiques (comme le chi²), l’approche par embeddings offre une alternative pour capturer les nuances sémantiques du texte et en extraire les termes les plus influents grâce aux mesures de centralité.
Prérequis
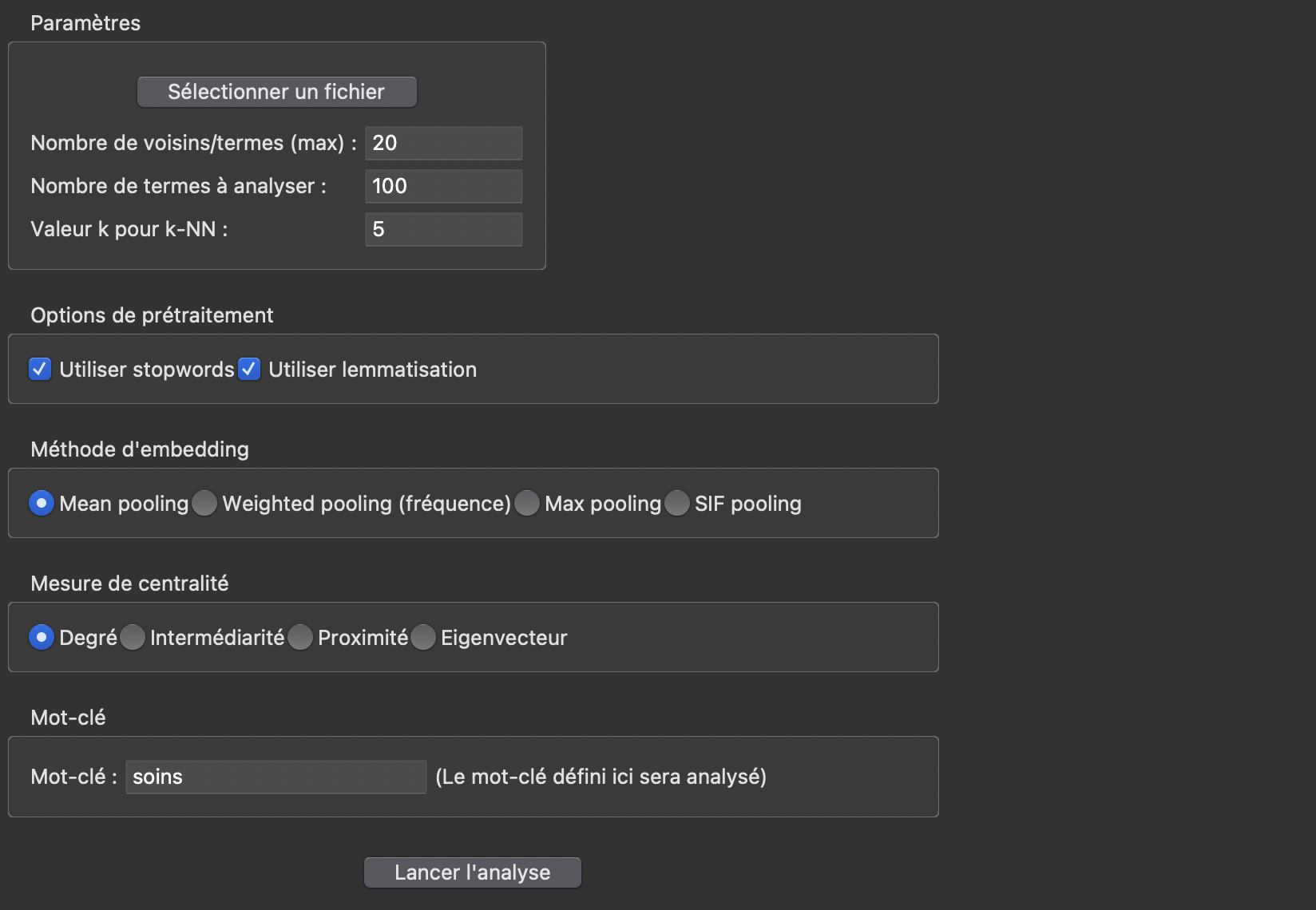
Pour faire tourner le script vous aurez besoin d’installer les librairies et d’importer votre corpus.
Les librairies
pip install torch transformers sentence-transformers networkx matplotlib pyvis pip install python-louvain pip install spacy python -m spacy download fr_core_news_sm
Le corpus
Votre corpus doit être enregistré au format .txt et structuré selon les exigences d’IRaMuTEQ, avec en première ligne de chaque article une ligne étoilées (****) pour séparer les articles.
1. Choix du k-nn
L’approche k‑NN consiste à connecter chaque nœud uniquement à ses k plus proches voisins, c’est-à-dire aux k nœuds présentant la plus forte similarité cosinus avec lui.
Plutôt que de construire un graphe complet où chaque nœud est potentiellement relié à tous les autres, le k‑NN permet de limiter le nombre de connexions et de rendre le réseau moins dense et plus intelligible.
L’approche k‑NN ne « parasite » pas l’analyse par centralité, elle la rend plutôt plus interprétable.
En effet, en limitant les connexions de chaque nœud à ses k plus proches voisins, le k‑NN réduit la densité du graphe et élimine les liens moins pertinents.
Toutefois, il est important de choisir judicieusement la valeur de k afin de ne pas perdre d’information importante. Un processus d’itération est recommandé.
2. Le processus d’embedding
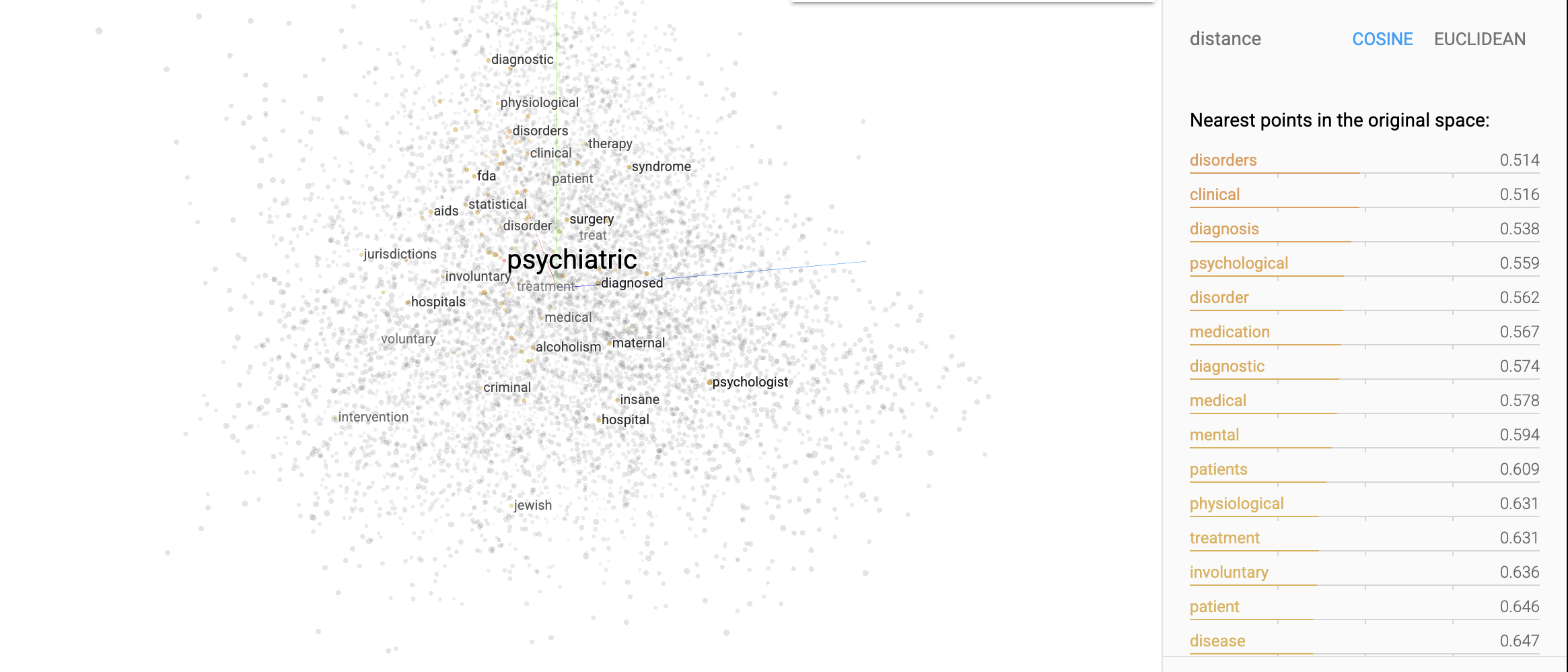
La construction initiale du graphe se fait à partir des similarités cosinus entre les vecteurs d’embedding, qui déterminent si deux termes sont reliés ou non.
Toutefois, une fois que ce graphe est constitué, les mesures de centralité sont calculées sur la structure globale du réseau.
Autrement dit, même si les liens sont définis par la similarité cosinus, la centralité ne se contente pas de refléter cette similarité, mais elle prend en compte la manière dont chaque nœud est positionné dans l’ensemble du réseau.
Par exemple, un nœud peut être connecté à des termes qui eux-mêmes sont très centraux, ce qui augmentera son score d’eigenvecteur. Ainsi, la représentation globale intègre à la fois l’information (la similarité cosinus) et la structure du réseau (via la centralité), permettant d’identifier des termes stratégiques au-delà d’une simple paire-à-paire comparaison.
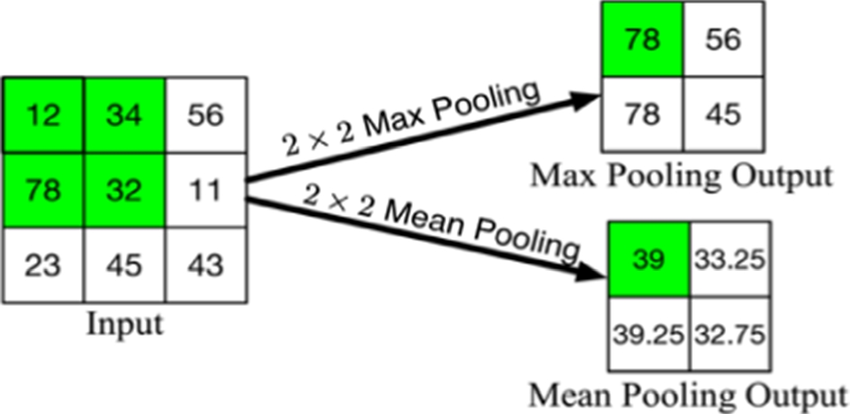
Le pooling, dans le contexte de l’embedding, est une technique permettant de réduire la dimensionnalité d’une séquence de vecteurs en une seule représentation fixe.
Par exemple, le « mean pooling » consiste à calculer la moyenne arithmétique de tous les vecteurs de tokens d’une phrase pour obtenir un vecteur unique qui résume l’information globale du texte. Le « mean pooling » est souvent privilégié pour sa robustesse et sa facilité de calcul, même s’il ne met pas en avant les signaux extrêmes comme le ferait, par exemple, le « max pooling ».
2.1 Mean pooling
La méthode « Mean pooling » consiste à calculer la moyenne arithmétique des vecteurs de chaque token d’une séquence pour obtenir une représentation unique du texte. Pour l’analyse textuelle, cette méthode est souvent efficace comme première approximation, mais elle peut parfois perdre des détails cruciaux dans des contextes où la variabilité lexicale est importante. Cependant, en se contentant de la moyenne, elle peut lisser des nuances importantes, en ne donnant pas suffisamment d’importance aux mots particulièrement porteurs de sens ou à ceux qui se distinguent dans leur contexte.
2.2 Weighted pooling
La méthode « Weighted pooling » utilise directement la fréquence des termes pour pondérer leurs vecteurs. Cela signifie que les mots qui apparaissent fréquemment dans la phrase auront un poids plus important dans le calcul de la moyenne pondérée, ce qui peut accentuer l’influence des mots courants. J’ai introduit cette méthode dans le script pour pouvoir la comparer à la méthode d’embedding SIF pooling.
À l’inverse, la méthode SIF pooling attribue un poids inversement proportionnel à la fréquence (avec un paramètre de lissage) et retire ensuite la composante commune, ce qui réduit l’influence des termes très fréquents. Ainsi, Weighted pooling amplifie l’importance des mots fréquents, tandis que SIF pooling tend à en atténuer l’impact pour mieux capter la nuance sémantique.
2.3 Max pooling
La méthode « Max pooling » fonctionne en sélectionnant, pour chaque dimension du vecteur d’embedding, la valeur maximale obtenue parmi tous les tokens d’une séquence. Cela permet de capturer le signal le plus fort présent dans chaque dimension, accentuant ainsi les caractéristiques les plus saillantes. Bien que cette méthode puisse mettre en évidence des aspects spécifiques et des indices forts dans le texte, elle risque d’ignorer l’information globale en se focalisant uniquement sur les valeurs extrêmes.
En conséquence, pour l’analyse textuelle, max pooling peut être utile pour repérer des indicateurs ponctuels forts, mais il peut aussi être sensible aux valeurs aberrantes et ne pas restituer toute la richesse contextuelle.
2.4 SIF pooling
La méthode « SIF pooling » (Smooth Inverse Frequency pooling) va plus loin que la simple moyenne en attribuant à chaque token un poids inversement proportionnel à sa fréquence, ce qui diminue l’influence des mots très communs. Cette approche permet d’obtenir une représentation plus fine et contextuelle. Dans le domaine de l’analyse textuelle, SIF pooling met en lumière des aspects importants du contenu tout en réduisant le bruit associé aux mots très fréquents.
3. La centralité
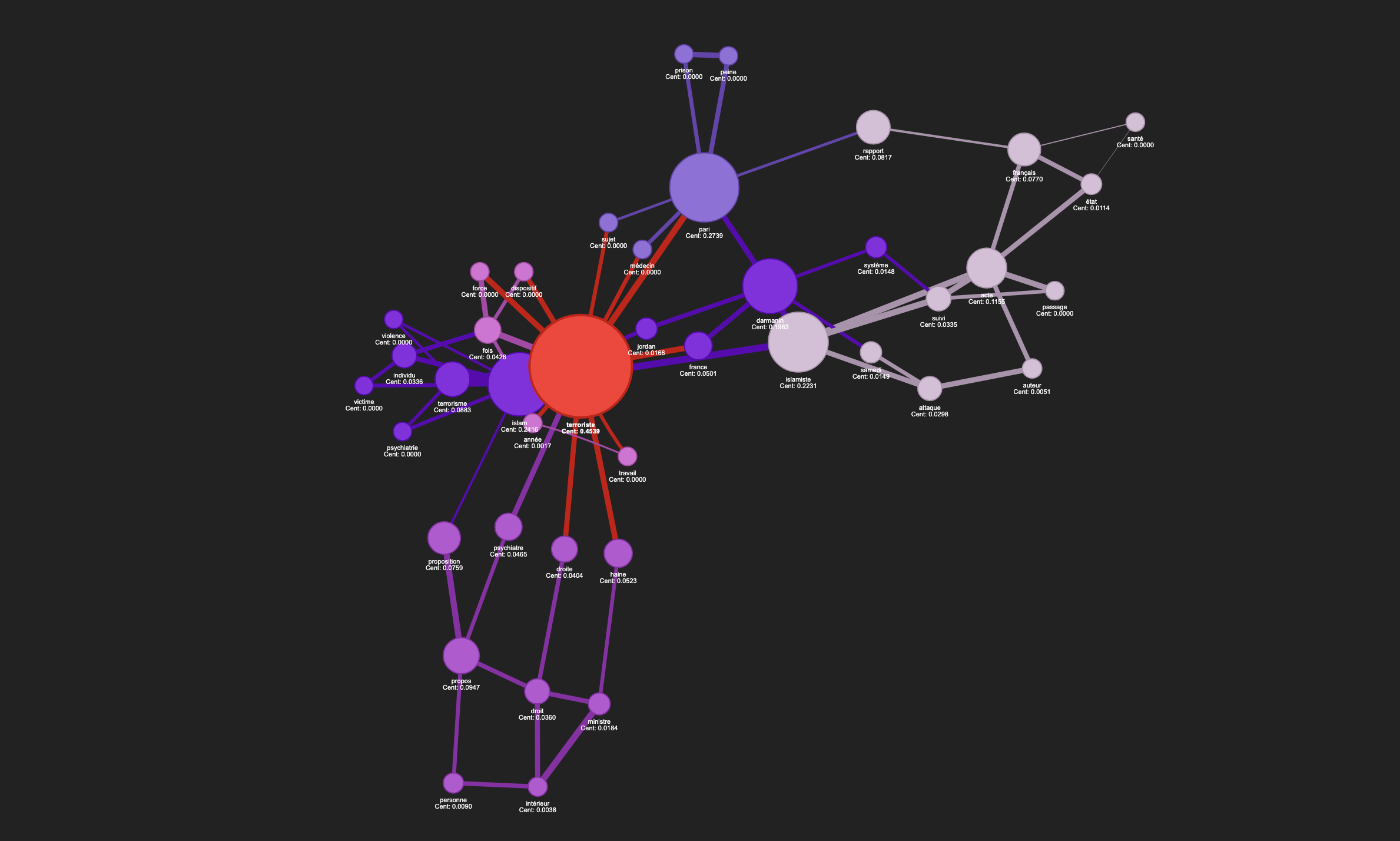
La centralité est une mesure qui quantifie l’importance ou l’influence d’un nœud dans un réseau. Par exemple, elle peut indiquer combien un terme est connecté aux autres (centralité de degré) ou à quel point il se trouve sur les chemins reliant d’autres nœuds (centralité d’intermédiarité).
Dans notre script, nous construisons un graphe sémantique où chaque nœud représente un terme extrait du corpus. La mesure de centralité (définie par l’utilisateur via l’interface, par exemple « degree » ou « betweenness ») est calculée pour chaque nœud afin d’identifier quels termes occupent des positions stratégiques dans le réseau. Ces scores sont ensuite affichés (et peuvent influencer la taille ou la couleur des nœuds) pour aider à interpréter l’importance relative des termes.
3.1 Choix de la mesure de centralité
La mesure à utiliser dépend du type d’information que vous souhaitez extraire.
La centralité de degré est simple et intuitive, la centralité d’intermédiarité est utile pour repérer les « ponts » entre sous-groupes, la centralité de proximité met en évidence l’accessibilité à l’information, et l’eigenvector centrality permet d’identifier les nœuds influents connectés à d’autres nœuds influents.
Le fait de partir d’un mot‑clé ne garantit pas que ce mot aura automatiquement le score de centralité le plus élevé.
Le choix de la mesure de centralité (degré, intermédiarité, proximité, eigenvecteur…) influence les résultats. Chaque mesure capture une facette différente de l’importance dans le réseau.
3.2 Centralité de degré
La centralité de degré d’un nœud mesure le nombre de connexions directes qu’il possède.
3.3 Centralité d’intermédiarité (Betweenness centrality)
La centralité d’intermédiarité mesure la fréquence à laquelle un nœud apparaît sur les plus courts chemins reliant tous les autres nœuds.
3.4 Centralité de proximité (Closeness centrality)
La centralité de proximité mesure la distance moyenne entre un nœud et tous les autres nœuds du graphe.
3.5 Centralité d’eigenvecteur (Eigenvector centrality)
La centralité d’eigenvecteur attribue à chaque nœud un score qui dépend non seulement du nombre de ses connexions, mais aussi de l’importance (ou score) des nœuds auxquels il est connecté.
Conclusion
En conclusion, l’approche exploratoire présentée dans cet article démontre le potentiel des techniques d’embedding, notamment via CamemBERT et les méthodes de pooling, pour construire des graphes sémantiques. Il serait toutefois intéressant de comparer ces résultats avec ceux obtenus par des méthodes plus classiques, basées sur les cooccurrences ou des tests statistiques comme le chi², afin d’évaluer la projection des mots sur le graphe.