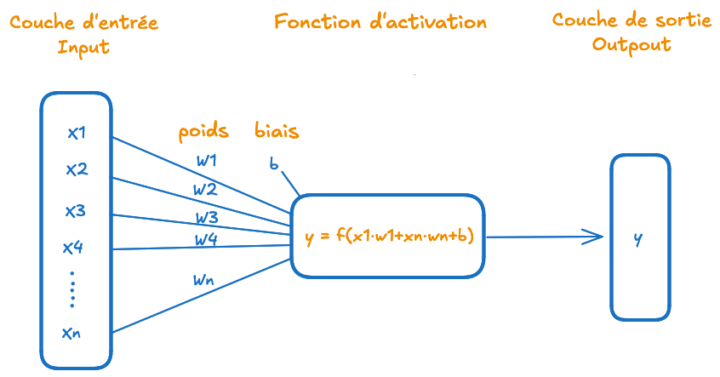
Comment fonctionne un neurone artificiel ?
Le neurone artificiel, s’inspire du fonctionnement des neurones biologiques. Dans cet article, nous allons présenter et modéliser un neurone artificiel en explorant ses paramètres de base et son processus de décision.
Historique du Perceptron
Le perceptron est l’un des premiers modèles de neurones artificiels. Il a été inventé en 1958 par Frank Rosenblatt, un psychologue et informaticien américain. Inspiré des recherches sur le cerveau humain, le perceptron était conçu pour effectuer des classifications binaires (0,1) à partir d’un ensemble de caractéristiques (features).
Modélisation du Perceptron monocouche
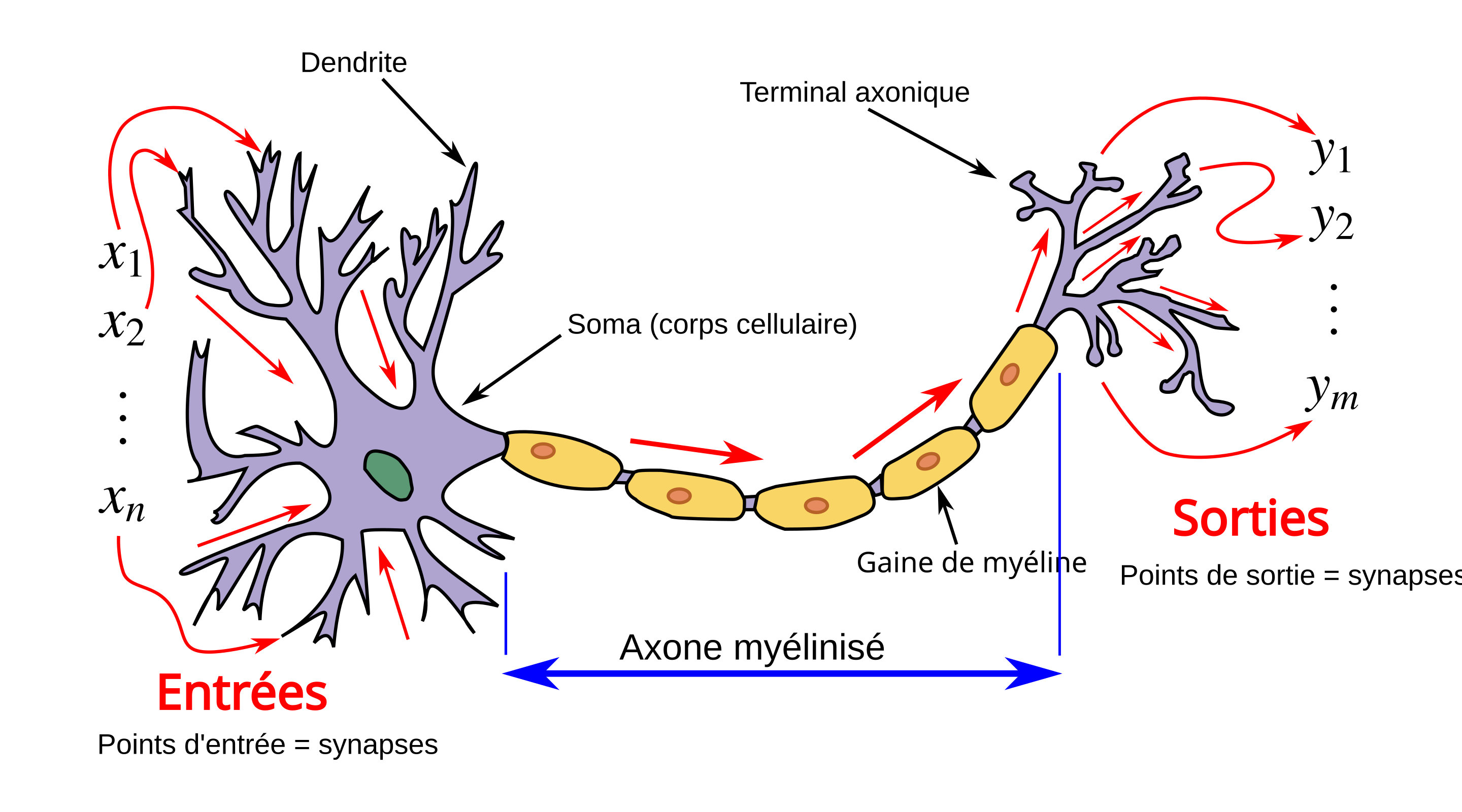
Le neurone artificiel est une tentative de modélisation mathématique du neurone biologique.
La couche d’entrée : Dendrites/Synapses => (xn)
Dans un neurone biologique, les dendrites reçoivent des signaux chimiques des neurotransmetteurs émis par d’autres neurones.
Ces signaux sont transmis au corps cellulaire sous forme d’impulsions électriques. Dans un neurone artificiel, ces signaux sont représentés par des entrées (x1, x2,… xn).
La fonction d’activation : Corps cellulaire et Axone => Décision
Dans un neurone biologique le corps cellulaire traite les signaux reçus des dendrites. Il calcule un “potentiel global” en intégrant toutes les impulsions électriques provenant des synapses.
Si ce potentiel dépasse un seuil d’activation, une impulsion électrique, appelée potentiel d’action, est déclenchée. L’impulsion est ensuite transmise le long de l’axone aux autres neurones ou cellules.
La couche de sortie : Axone => y
L’axone transmet le signal lorsque le seuil d’activation est atteint. De manière similaire, un neurone artificiel utilise une fonction d’activation pour décider si le signal sera transmis ou non. Une fonction d’activation seuil retourne 1 (signal envoyé) ou 0 (aucun signal).
Un neurone artificiel est une abstraction mathématique du neurone biologique :
- Il reçoit des entrées (xn) correspondant aux signaux des dendrites.
- Il les pondère à l’aide de poids (wn), qui jouent le rôle des synapses.
- Il calcule une somme pondérée (z), équivalente au potentiel global dans le corps cellulaire.
- Il utilise une fonction d’activation (par exemple, une fonction seuil) pour décider si le signal est transmis.
- La sortie (y) est l’équivalent de l’impulsion envoyée par l’axone.
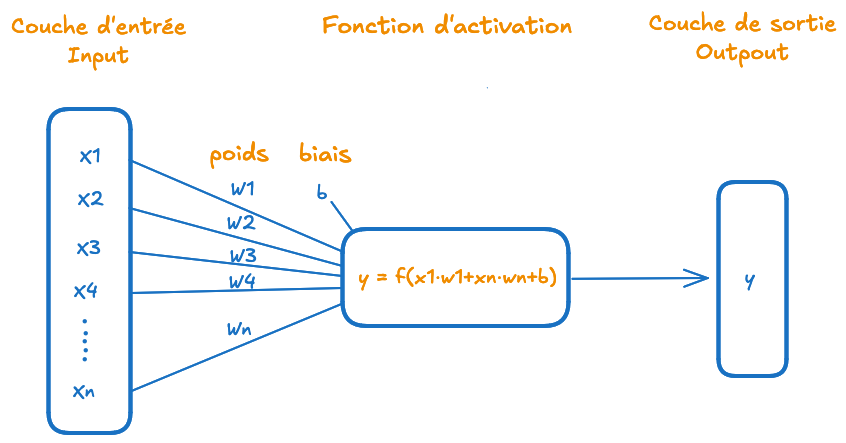
- Entrées/features (x1,x2,…,xn).
- Poids (w1,w2,…,wn).
- Biais (b).
- Fonction d’activation (f).
- Sortie (y), qui est la valeur finale produite par le neurone.
Le paramètre poids (w) dans un neurone artificiel
Un poids dans un réseau neuronal est un paramètre qui détermine l’importance ou l’influence d’une entrée (x1, x2) sur la sortie du neurone. Chaque entrée xi est multipliée par son poids wi, ce qui signifie que :
- Si le poids wi est élevé, l’entrée xi aura alors un impact important sur la “décision” du neurone.
- Si le poids wi est faible ou négatif, l’entrée xi aura moins d’impact.
Exemple :
- Si x1 représente le temps d’étude d’un étudiant, et que w1=2, cela indique que le temps d’étude a une grande influence sur le résultat.
- Si w1=0.1, cela signifie que le temps d’étude est presque insignifiant dans la décision.
L’objectif final du processus d’apprentissage est de trouver une configuration de poids qui permet au réseau neuronal de produire des prédictions avec l’erreur la plus faible possible. Initialement les poids sont générés aléeatoirement, puis par ajustements les poids atteignent un “équilibre”, où les prédictions deviennent suffisamment précises. Nous reviendrons sur ce paramètre dans un article spécifique.
Le paramètre de biais (b) dans un neurone artificiel
Le biais peut être vu comme un paramètre qui permet d’ajuster ou de “corriger” le comportement du neurone artificiel dans des situations où les entrées seules ne suffisent pas à produire des prédictions précises. Cela est particulièrement utile lorsque les entrées xn manquent de diversité ou lorsque toutes les pondérations (wn) sont faibles
Dans un réseau neuronal, chaque couche (à l’exception de la couche d’entrée) inclut un biais. Initialement, le biais est défini de façon aléatoire, mais il est ajusté au cours de l’entraînement par la backpropagation, en suivant l’algorithme de descente de gradient, pour réduire l’erreur entre les prédictions du réseau et les données réelles.
La modélisation commence par le calcul de (z), qui représente la somme pondérée des entrées et du biais.
Une fois que nous avons calculé (z), qui représente la somme pondérée des entrées plus le biais, nous appliquons une fonction d’activation (f) pour obtenir la sortie (y) qui est la “prédiction” .
La modélisation peut donc s’écrire :
“Y EST FONCTION DE Z”
( est la somme pondérée des entrées (x1,x2,…,xn), où chaque entrée est multipliée par son poids (w1,w2,…,wn) et un biais (b)
- f est la fonction d’activation, qui transforme (z) en une sortie utilisable par le neurone suivant ou comme résultat final.
- Il faut préciser que le perceptron simple (une couche/monocouche) ne peut pas modéliser des relations complexes ou non linéaires.
La fonction d’activation est une fonction mathématique qui transforme la somme pondérée des entrées d’un neurone artificiel en une sortie, (souvent non linéaire, sauf dans le cas du perceptron monocouche), pour permettre au réseau de modéliser des relations complexes.
Autrement écrit :
Dans le perceptron simple, f(z) est une fonction seuil (dite aussi binaire), retournant 1 si le seuil est atteint (z ≥ 0), ou 0 sinon.
La fonction d’activation transforme la somme pondérée (z) en une sortie binaire (1 ou 0), permettant ainsi de classer les données dans (uniquement) deux catégories distinctes.
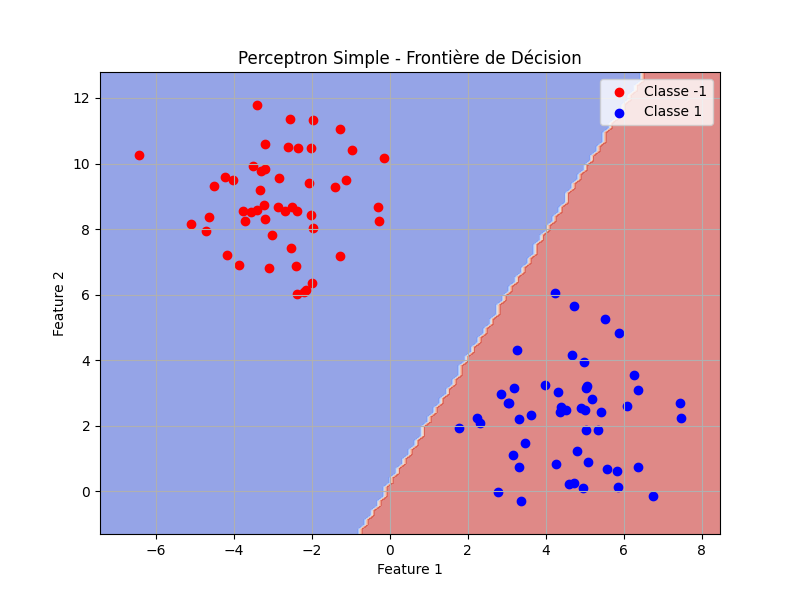
Le perceptron monocouche reste un modèle linéaire, car la relation entre les entrées (xn) et la sortie (y) est définie par une frontière de décision linéaire.
Exemple concret
Si un neurone artificiel reçoit deux entrées (x1 = 2, x2 = 3), avec des poids (w1 = 0.5, w2 = −0.6), et un biais (b = 0.2), alors :
- La somme pondérée est : z = ( 0.5 * 2 ) + ( −0.6 * 3 ) + 0.2 = 1.0 − 1.8 + 0.2 = −0.6
- En activant la fonction seuil, alors, puisque z = −0.6 , la sortie (y) sera .

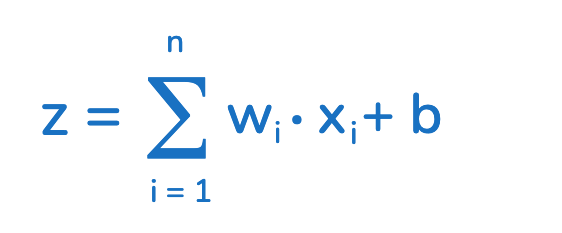
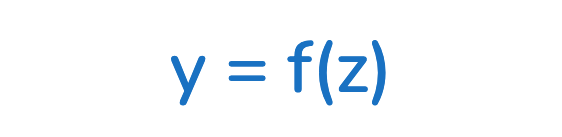
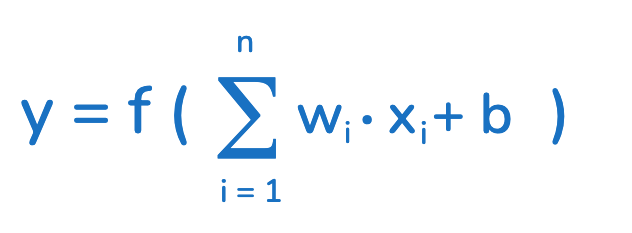
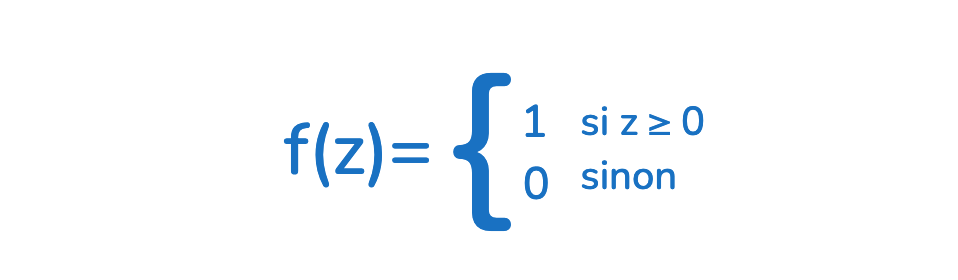
[…] Bien que l’architecture des “Larges Langage Modèles” (LLM) s’inspire du fonctionnement du neurone, l’analogie s’arrête là. Ces modèles ne possèdent aucune représentation du monde, […]